An integral is a mathematical object that can be interpreted as an area or a generalization of area. Integrals, together with derivatives, are the fundamental objects of calculus. Other words for integral include antiderivative and primitive. The Riemann integral is the simplest integral definition and the only one usually encountered in physics and elementary calculus. In fact, according to Jeffreys and Jeffreys (1988, p. 29), "it appears that cases where these methods [i.e., generalizations of the Riemann integral] are applicable and Riemann's [definition of the integral] is not are too rare in physics to repay the extra difficulty."

The Riemann integral of the function over from to is written

(1)

Note that if , the integral is written simply

(2)

as opposed to .

Every definition of an integral is based on a particular measure. For instance, the Riemann integral is based on Jordan measure, and the Lebesgue integral is based on Lebesgue measure. The process of computing an integral is called integration (a more archaic term for integration is quadrature), and the approximate computation of an integral is termed numerical integration.

There are two classes of (Riemann) integrals: definite integrals such as (1), which have upper and lower limits, and indefinite integrals, such as

(3)

which are written without limits. The first fundamental theorem of calculus allows definite integrals to be computed in terms of indefinite integrals, since if is the indefinite integral for , then

(4)

Since the derivative of a constant is zero, indefinite integrals are defined only up to an arbitrary constant of integration , i.e.,

(5)

Wolfram Research maintains a web site http://integrals.wolfram.com/ that can find the indefinite integral of many common (and not so common) functions.

Differentiating integrals leads to some useful and powerful identities. For instance, if is continuous, then

(6)

which is the first fundamental theorem of calculus. Other derivative-integral identities include

(7)

the Leibniz integral rule

(8)

(Kaplan 1992, p. 275), its generalization

(9)

(Kaplan 1992, p. 258), and

(10)

as can be seen by applying (9) on the left side of (10) and using partial integration.

Other integral identities include

(11)

(12)

			(13)
			(14)

and the amusing integral identity

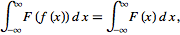(15)

where is any function and

(16)

as long as and is real (Glasser 1983).

Integrals with rational exponents can often be solved by making the substitution , where is the least common multiple of the denominator of the exponents.

Beyer, W. H. "Integrals." CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 233-296, 1987.

Boros, G. and Moll, V. Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge, England: Cambridge University Press, 2004.

Bronstein, M. Symbolic Integration I: Transcendental Functions. New York: Springer-Verlag, 1996.

Dubuque, W. G. "Re: Integrals done free on the Web." math-fun@cs.arizona.edu posting, Sept. 24, 1996.

Glasser, M. L. "A Remarkable Property of Definite Integrals." Math. Comput. 40, 561-563, 1983.

Gordon, R. A. The Integrals of Lebesgue, Denjoy, Perron, and Henstock. Providence, RI: Amer. Math. Soc., 1994.

Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.

Jeffreys, H. and Jeffreys, B. S. Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, p. 29, 1988.

Kaplan, W. Advanced Calculus, 4th ed. Reading, MA: Addison-Wesley, 1992.

Piessens, R.; de Doncker, E.; Uberhuber, C. W.; and Kahaner, D. K. QUADPACK: A Subroutine Package for Automatic Integration. New York: Springer-Verlag, 1983.

Ritt, J. F. Integration in Finite Terms: Liouville's Theory of Elementary Methods. New York: Columbia University Press, p. 37, 1948.

Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 145, 1993.

Wolfram Research. "The Integrator." http://integrals.wolfram.com/.

CITE THIS AS:

Weisstein, Eric W. "Integral." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Integral.html