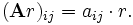Matrix multiplication

From Wikipedia, the free encyclopedia

In mathematics, matrix multiplication is the operation of multiplying a matrix with either a scalar or another matrix. This article gives an overview of the various ways to perform matrix multiplication.

[edit] Ordinary matrix product

The ordinary matrix product is the most often used and the most important way to multiply matrices. It is defined between two matrices only if the width of the first matrix equals the height of the second matrix. Multiplying an m×n matrix with an n×p matrix results in an m×p matrix. If many matrices are multiplied together, and their dimensions are written in a list in order, e.g. m×n, n×p, p×q, q×r, the size of the result is given by the first and the last numbers (m×r), and the values surrounding each comma must match for the result to be defined. The ordinary matrix product is not commutative.

$\overset{3\times 4 \text{ matrix}}{\begin{bmatrix} \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot \\ \color{Blue} 1 & \color{Blue} 2 & \color{Blue} 3 & \color{Blue} 4 \\ \end{bmatrix}} \overset{4\times 5\text{ matrix}}{\begin{bmatrix} \cdot & \cdot & \cdot & \color{Red}a & \cdot \\ \cdot & \cdot & \cdot & \color{Red}b & \cdot \\ \cdot & \cdot & \cdot & \color{Red}c & \cdot \\ \cdot & \cdot & \cdot & \color{Red}d & \cdot \\ \end{bmatrix}} = \overset{3\times 5\text{ matrix}}{ \begin{bmatrix} \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & x_{3,4} & \cdot \\ \end{bmatrix}}$

The element $x 3,4$ of the above matrix product is computed as follows

$x_{3,4} = ({\color{Blue}1}, {\color{Blue}2}, {\color{Blue}3}, {\color{Blue}4})\cdot ({\color{Red}a}, {\color{Red}b}, {\color{Red}c}, {\color{Red}d}) = {\color{Blue} 1}\times{\color{Red} a} +{\color{Blue} 2}\times{\color{Red} b} +{\color{Blue} 3}\times{\color{Red} c} +{\color{Blue} 4}\times{\color{Red} d}.$

The first coordinate in matrix notation denotes the row and the second the column; this order is used both in indexing and in giving the dimensions. The element $x_{{\color{Blue}i}{\color{Red}j}}$ at the intersection of row $i$ and column $j$ of the product matrix is the dot product (inner product) of row $i$ of the first matrix and column $j$ of the second matrix. This explains why the width and the height of the matrices being multiplied must match: otherwise the dot product is not defined.

The figure to the right illustrates the product of two matrices A and B, showing how each intersection in the product matrix corresponds to a row of A and a column of B. The size of the output matrix is always the largest possible, i.e. for each row of A and for each column of B there are always corresponding intersections in the product matrix. The product matrix AB consists of all combinations of dot products of rows of A and columns of B.

The values at the intersections marked with circles are:

$\begin{align} {\color{Red}x_{1,2}} &= (a_{1,1}, a_{1,2})\cdot(b_{1,2}, b_{2,2}) \\ &= a_{1, 1}b_{1,2} + a_{1,2}b_{2, 2} \\ {\color{Blue}x_{3,3}} &= (a_{3,1}, a_{3, 2})\cdot(b_{1, 3}, b_{2, 3}) \\ &= a_{3, 1}b_{1,3} + a_{3,2}b_{2, 3}. \end{align}$

[edit] Formal definition

Formally, for

$A \in {\mathbb R}^{m \times n}$ , $B \in {\mathbb R}^{n \times p}$

then

$(AB) \in {\mathbb R}^{m \times p}$

where the elements of $A B$ are given by

$(AB)_{i,j} = \sum_{r=1}^n A_{i,r}B_{r,j}$

for each pair i and j with 1 ≤ i ≤ m and 1 ≤ j ≤ p. The algebraic system of "matrix units" summarizes the abstract properties of this kind of multiplication.

[edit] Relationship with the inner product and the outer product

The Euclidean inner product and outer product are the simplest special cases of the ordinary matrix product. The inner product of two column vectors $A$ and $B$ is $A\cdot B = A^TB$ , where T denotes the matrix transpose. More explicitly,

$A\cdot B = A^TB = \begin{bmatrix}a_1 & a_2 & \cdots & a_n\end{bmatrix} \begin{bmatrix}b_1 \\ b_2 \\ \vdots \\ b_n\end{bmatrix} = \begin{bmatrix} a_1b_1+a_2b_2+\cdots+a_nb_n \end{bmatrix}.$

The outer product is $A\otimes B = AB^T$ , where

$AB^T = \begin{bmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{bmatrix} \begin{bmatrix}b_1 & b_2 & \cdots & b_n\end{bmatrix} = \begin{bmatrix} a_1 b_1 & a_1 b_2 & \cdots & a_1 b_n \\ a_2 b_1 & a_2 b_2 & \cdots & a_2 b_n \\ \vdots & \vdots & \ddots & \vdots \\ a_n b_1 & a_n b_2 & \cdots & a_n b_n \\ \end{bmatrix}.$

Matrix multiplication can be viewed in terms of these two operations by considering how the matrix product works on block matrices.

Decomposing A into row vectors and B into column vectors:

$\mathbf{A} = \begin{bmatrix} {\color{Red} a_{1,1}} & {\color{Red}a_{1, 2}} & \cdots & {\color{Red} a_{1, n}} \\ {\color{ForestGreen} a_{2,1}} & {\color{ForestGreen} a_{2, 2}} & \cdots & {\color{ForestGreen} a_{2, n}} \\ \vdots & \vdots & \ddots & \vdots \\ {\color{Blue} a_{m, 1}} & {\color{Blue} a_{m, 2}} & \cdots & {\color{Blue} a_{m, n}} \end{bmatrix} = \begin{bmatrix} {\color{Red} A_1} \\ {\color{ForestGreen} A_2} \\ \vdots \\ {\color{Blue} A_m} \end{bmatrix}$

$\mathbf{B} = \begin{bmatrix} {\color{Red}b_{1,1}} & {\color{ForestGreen}b_{1, 2}} & \cdots & {\color{Blue}b_{1, p}} \\ {\color{Red}b_{2,1}} & {\color{ForestGreen}b_{2, 2}} & \cdots & {\color{Blue}b_{2, p}} \\ \vdots & \vdots & \ddots & \vdots \\ {\color{Red}b_{n, 1}} & {\color{ForestGreen}b_{m, 2}} & \cdots & {\color{Blue}b_{n, p}} \end{bmatrix} = \begin{bmatrix} {\color{Red} B_1} & {\color{ForestGreen} B_2} & \cdots & {\color{Blue} B_p} \end{bmatrix}$

where

$A_i = \begin{bmatrix}a_{i, 1} & a_{i, 2} & \cdots & a_{i, n} \end{bmatrix}$

$B_i = \begin{bmatrix}b_{1, i} & b_{2, i} & \cdots & b_{n, i}\end{bmatrix}^T.$

The method in the introduction was:

$\mathbf{AB} = \begin{bmatrix} A_1 \\ A_2 \\ \vdots \\ A_m \end{bmatrix} \begin{bmatrix} B_1 & B_2 & \dots & B_p \end{bmatrix} = \begin{bmatrix} (A_1 \cdot B_1) & (A_1 \cdot B_2) & \dots & (A_1 \cdot B_p) \\ (A_2 \cdot B_1) & (A_2 \cdot B_2) & \dots & (A_2 \cdot B_p) \\ \vdots & \vdots & \ddots & \vdots \\ (A_m \cdot B_1) & (A_m \cdot B_2) & \dots & (A_m \cdot B_p) \end{bmatrix}.$

This is an outer product where the real product inside is replaced with the inner product. In general, block matrix multiplication works exactly like ordinary matrix multiplication, but the real product inside is replaced with the matrix product.

An alternative method results when the decomposition is done the other way around (A decomposed into column vectors and B into row vectors):

$\mathbf{AB} = \begin{bmatrix} A_1 & A_2 & \cdots & A_n \end{bmatrix} \begin{bmatrix} B_1 \\ B_2 \\ \vdots \\ B_n\end{bmatrix} = A_1 \otimes B_1 + A_2 \otimes B_2 + \cdots + A_n \otimes B_n.$

This method emphasizes the effect of individual column/row pairs on the result, which is a useful point of view with e.g. covariance matrices, where each such pair corresponds to the effect of a single sample point. An example for a small matrix:

$\begin{bmatrix} {\color{Red}1} & {\color{ForestGreen}2} & {\color{Blue}3} \\ {\color{Red}4} & {\color{ForestGreen}5} & {\color{Blue}6} \\ {\color{Red}7} & {\color{ForestGreen}8} & {\color{Blue}9} \\ \end{bmatrix} \begin{bmatrix} {\color{Red}a} & {\color{Red}d} \\ {\color{ForestGreen}b} & {\color{ForestGreen}e} \\ {\color{Blue}c} & {\color{Blue}f} \\ \end{bmatrix} = \begin{bmatrix} {\color{Red}1a} & {\color{Red}1d} \\ {\color{Red}4a} & {\color{Red}4d} \\ {\color{Red}7a} & {\color{Red}7d} \\ \end{bmatrix}+ \begin{bmatrix} {\color{ForestGreen}2b} & {\color{ForestGreen}2e} \\ {\color{ForestGreen}5b} & {\color{ForestGreen}5e} \\ {\color{ForestGreen}8b} & {\color{ForestGreen}8e} \\ \end{bmatrix}+ \begin{bmatrix} {\color{Blue}3c} & {\color{Blue}3f} \\ {\color{Blue}6c} & {\color{Blue}6f} \\ {\color{Blue}9c} & {\color{Blue}9f} \\ \end{bmatrix}.$

One more useful decomposition results when B is decomposed into columns and A is left undecomposed. Then A is seen to act separately on each column of B, transforming them in parallel. Conversely, B acts separately on each row of A.

If x is a vector and A is decomposed into columns, then $\mathbf{A}x = A_1x_1+A_2x_2+\cdots+A_nx_n$ . The column vectors of A give directions and units for coordinate axes and the elements of x are coordinates on the corresponding axes. $\mathbf{A}x$ is then the vector which has those coordinates in the coordinate system given by the column vectors of A.

[edit] Properties

Matrix multiplication is not generally commutative

$AB \ne BA$

If A and B are both n x n matrices, the determinant of their product is independent of the order of the matrices in the product.

$\;\!\det(AB) = \det(BA)$

If both matrices are diagonal square matrices of the same dimension, their product is commutative.^[1]

If A is a matrix representative of a linear transformation L and B is a matrix representative of a linear transformation P then AB is a matrix representative of a linear transform P followed by the linear transformation L.
Matrix multiplication is associative:

$\ \mathbf{A} ( \mathbf{B C} ) = ( \mathbf{A B} ) \mathbf{C}$

Matrix multiplication is distributive over matrix addition:

$\ \mathbf{A} ( \mathbf{B} + \mathbf{C} ) = \mathbf{A B} + \mathbf{AC}$

$\ ( \mathbf{A} + \mathbf{B} ) \mathbf{C} = \mathbf{A C} + \mathbf{B C}$ .

If the matrix is defined over a field (for example, over the Real or Complex fields), then it is compatible with scalar multiplication in that field.

$\ c ( \mathbf{A B} ) = ( c \mathbf{A} ) \mathbf{B}$

$\ ( \mathbf{A} c ) \mathbf{B} = \mathbf{A} ( c \mathbf{B} )$

$\ ( \mathbf{A B} ) c = \mathbf{A} ( \mathbf{B} c )$

where c is a scalar.

[edit] Algorithms for efficient matrix multiplication

The complexity of square matrix multiplication, if carried out naively, is $O (n 3)$ , but more efficient algorithms do exist. Strassen's algorithm, devised by Volker Strassen in 1969 and often referred to as "fast matrix multiplication", is based on a clever way of multiplying two 2 × 2 matrices which requires only 7 multiplications (instead of the usual 8), at the expense of several additional addition and subtraction operations. Applying this trick recursively gives an algorithm with a multiplicative cost of $O( n^{\log_{2}7}) \approx O(n^{2.807})$ . Strassen's algorithm is awkward to implement, compared to the naive algorithm, and it lacks numerical stability. Nevertheless, it is beginning to appear in libraries such as BLAS, where it is computationally interesting for matrices with dimensions n > 100^[2], and is very useful for large matrices over exact domains such as finite fields, where numerical stability is not an issue. The computational complexity for multiplying rectangular matrices (one m×p-matrix with one p×n-matrix) is O(mnp).

The currently $O (n k)$ algorithm with the lowest known exponent k is the Coppersmith–Winograd algorithm. It was presented by Don Coppersmith and Shmuel Winograd in 1990, has an asymptotic complexity of O(n^2.376). It is similar to Strassen's algorithm: a clever way is devised for multiplying two k × k matrices with fewer than k³ multiplications, and this technique is applied recursively. It improves on the constant factor in Strassen's algorithm, reducing it to 4.537. However, the constant term implied in the O(n^2.376) result is so large that the Coppersmith–Winograd algorithm is only worthwhile for matrices that are too large to handle on present-day computers.^[3]

Since any algorithm for multiplying two n × n matrices has to process all 2 × n² entries, there is an asymptotic lower bound of $ω(n 2)$ operations. Raz (2002) proves a lower bound of $Ω(m 2 log m)$ for bounded coefficient arithmetic circuits over the real or complex numbers.

Cohn et al. (2003, 2005) put methods, such as the Strassen and Coppersmith–Winograd algorithms, in an entirely different group-theoretic context. They show that if families of wreath products of Abelian with symmetric groups satisfying certain conditions exists, matrix multiplication algorithms with essential quadratic complexity exist. Most researchers believe that this is indeed the case^[4] - a lengthy attempt at proving this was undertaken by the late Jim Eve.^[5]

Because of the nature of matrix operations and the layout of matrices in memory, it is typically possible to gain substantial performance gains through use of parallelisation and vectorization. It should therefore be noted that some lower time-complexity algorithms on paper may have indirect time complexity costs on real machines.

[edit] Relationship to linear transformations

Matrices offer a concise way of representing linear transformations between vector spaces, and (ordinary) matrix multiplication corresponds to the composition of linear transformations. This will be illustrated here by means of an example using three vector spaces of specific dimensions, but the correspondence applies equally to any other choice of dimensions.

Let X, Y, and Z be three vector spaces, with dimensions 4, 2, and 3, respectively, all over the same field, for example the real numbers. The coordinates of a point in X will be denoted as x_i, for i = 1 to 4, and analogously for the other two spaces.

Two linear transformations are given: one from Y to X, which can be expressed by the system of linear equations

$\begin{align} x_1 & = a_{1,1}y_1+a_{1,2}y_2 \\ x_2 & = a_{2,1}y_1+a_{2,2}y_2 \\ x_3 & = a_{3,1}y_1+a_{3,2}y_2 \\ x_4 & = a_{4,1}y_1+a_{4,2}y_2 \end{align}$

and one from Z to Y, expressed by the system

$\begin{align} y_1 & = b_{1,1}z_1+b_{1,2}z_2+b_{1,3}z_3 \\ y_2 & = b_{2,1}z_1+b_{2,2}z_2+b_{2,3}z_3 \end{align}$

These two transformations can be composed to obtain a transformation from Z to X. By substituting, in the first system, the right-hand sides of the equations of the second system for their corresponding left-hand sides, the x_i can be expressed in terms of the z_k:

$\begin{align} x_1 & = a_{1,1}(b_{1,1}z_1{+}b_{1,2}z_2{+}b_{1,3}z_3)+a_{1,2}(b_{2,1}z_1{+}b_{2,2}z_2{+}b_{2,3}z_3) \\ & = (a_{1,1} b_{1,1}{+}a_{1,2} b_{2,1})z_1+(a_{1,1} b_{1,2}{+}a_{1,2} b_{2,2})z_2+(a_{1,1} b_{1,3}{+}a_{1,2} b_{2,3})z_3 \\ x_2 & = a_{2,1}(b_{1,1}z_1{+}b_{1,2}z_2{+}b_{1,3}z_3)+a_{2,2}(b_{2,1}z_1{+}b_{2,2}z_2{+}b_{2,3}z_3) \\ & = (a_{2,1} b_{1,1}{+}a_{2,2} b_{2,1})z_1+(a_{2,1} b_{1,2}{+}a_{2,2} b_{2,2})z_2+(a_{2,1} b_{1,3}{+}a_{2,2} b_{2,3})z_3 \\ x_3 & = a_{3,1}(b_{1,1}z_1{+}b_{1,2}z_2{+}b_{1,3}z_3)+a_{3,2}(b_{2,1}z_1{+}b_{2,2}z_2{+}b_{2,3}z_3) \\ & = (a_{3,1} b_{1,1}{+}a_{3,2} b_{2,1})z_1+(a_{3,1} b_{1,2}{+}a_{3,2} b_{2,2})z_2+(a_{3,1} b_{1,3}{+}a_{3,2} b_{2,3})z_3 \\ x_4 & = a_{4,1}(b_{1,1}z_1{+}b_{1,2}z_2{+}b_{1,3}z_3)+a_{4,2}(b_{2,1}z_1{+}b_{2,2}z_2{+}b_{2,3}z_3) \\ & = (a_{4,1} b_{1,1}{+}a_{4,2} b_{2,1})z_1+(a_{4,1} b_{1,2}{+}a_{4,2} b_{2,2})z_2+(a_{4,1} b_{1,3}{+}a_{4,2} b_{2,3})z_3 \end{align}$

These three systems can be written equivalently in matrix–vector notation – thereby reducing each system to a single equation – as follows:

$\begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} a_{1,1} & a_{1,2} \\ a_{2,1} & a_{2,2} \\ a_{3,1} & a_{3,2} \\ a_{4,1} & a_{4,2} \end{bmatrix} \begin{bmatrix} y_1 \\ y_2 \end{bmatrix}$

$\begin{bmatrix} y_1 \\ y_2 \end{bmatrix} = \begin{bmatrix} b_{1,1} & b_{1,2} & b_{1,3} \\ b_{2,1} & b_{2,2} & b_{2,3} \end{bmatrix} \begin{bmatrix} z_1 \\ z_2 \\ z_3 \end{bmatrix}$

$\begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} a_{1,1} b_{1,1}{+}a_{1,2} b_{2,1} & a_{1,1} b_{1,2}{+}a_{1,2} b_{2,2} & a_{1,1} b_{1,3}{+}a_{1,2} b_{2,3} \\ a_{2,1} b_{1,1}{+}a_{2,2} b_{2,1} & a_{2,1} b_{1,2}{+}a_{2,2} b_{2,2} & a_{2,1} b_{1,3}{+}a_{2,2} b_{2,3} \\ a_{3,1} b_{1,1}{+}a_{3,2} b_{2,1} & a_{3,1} b_{1,2}{+}a_{3,2} b_{2,2} & a_{3,1} b_{1,3}{+}a_{3,2} b_{2,3} \\ a_{4,1} b_{1,1}{+}a_{4,2} b_{2,1} & a_{4,1} b_{1,2}{+}a_{4,2} b_{2,2} & a_{4,1} b_{1,3}{+}a_{4,2} b_{2,3} \end{bmatrix} \begin{bmatrix} z_1 \\ z_2 \\ z_3 \end{bmatrix}$

Representing these three equations symbolically and more concisely as

$\begin{align} \mathbf{x} = \mathbf{Ay} \\ \mathbf{y} = \mathbf{Bz} \\ \mathbf{x} = \mathbf{Cz} \\ \end{align}$

inspection of the entries of matrix C reveals that C = AB.

This can be used to formulate a more abstract definition of matrix multiplication, given the special case of matrix–vector multiplication: the product AB of matrices A and B is the matrix C such that for all vectors z of the appropriate shape Cz = A(Bz).

[edit] Scalar multiplication

The scalar multiplication of a matrix A = (a_ij) and a scalar r gives a product r A of the same size as A. The entries of r A are given by

$(r\mathbf{A})_{ij} = r \cdot a_{ij}. \,$

For example, if

$\mathbf{A}=\begin{bmatrix} a & b \\ c & d \end{bmatrix}$

then

$p \cdot \mathbf{A}=\begin{bmatrix} p \cdot a & p \cdot b \\ p \cdot c & p \cdot d \end{bmatrix}$

If we are concerned with matrices over a more general ring, then the above multiplication is the left multiplication of the matrix A with scalar p while the right multiplication is defined to be

$(\mathbf{A}r)_{ij} = a_{ij} \cdot r. \,$

When the underlying ring is commutative, for example, the real or complex number field, the two multiplications are the same. However, if the ring is not commutative, such as the quaternions, they may be different. For example

$i\begin{bmatrix} i & 0 \\ 0 & j \\ \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & k \\ \end{bmatrix} \ne \begin{bmatrix} -1 & 0 \\ 0 & -k \\ \end{bmatrix} = \begin{bmatrix} i & 0 \\ 0 & j \\ \end{bmatrix}i.$

[edit] Hadamard product

[edit] Kronecker product

Main article: Kronecker product

For any two arbitrary matrices A and B, we have the direct product or Kronecker product A ⊗ B defined as

$\begin{bmatrix} a_{11}B & a_{12}B & \cdots & a_{1n}B \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1}B & a_{m2}B & \cdots & a_{mn}B \end{bmatrix}.$

If A is an m-by-n matrix and B is a p-by-q matrix, then their Kronecker product A ⊗ B is an mp-by-nq matrix.

The Kronecker product is not commutative.

For example

$\begin{bmatrix} 1 & 2 \\ 3 & 1 \\ \end{bmatrix} \otimes \begin{bmatrix} 0 & 3 \\ 2 & 1 \\ \end{bmatrix} = \begin{bmatrix} 1\cdot 0 & 1\cdot 3 & 2\cdot 0 & 2\cdot 3 \\ 1\cdot 2 & 1\cdot 1 & 2\cdot 2 & 2\cdot 1 \\ 3\cdot 0 & 3\cdot 3 & 1\cdot 0 & 1\cdot 3 \\ 3\cdot 2 & 3\cdot 1 & 1\cdot 2 & 1\cdot 1 \\ \end{bmatrix} = \begin{bmatrix} 0 & 3 & 0 & 6 \\ 2 & 1 & 4 & 2 \\ 0 & 9 & 0 & 3 \\ 6 & 3 & 2 & 1 \end{bmatrix}.$

If A and B represent linear transformations V₁ → W₁ and V₂ → W₂, respectively, then A ⊗ B represents the tensor product of the two maps, V₁ ⊗ V₂ → W₁ ⊗ W₂.

[edit] Common properties

The Wikibook The Book of Mathematical Proofs has a page on the topic of

Proofs of properties of matrices

If A, B and C are matrices with appropriate dimensions defined over a field (e.g. $\mathbb{Q}, \mathbb{R} \text{ or } \mathbb{C}$ ) where c is a scalar in that field, then for all three types of multiplication:

Matrix multiplication is associative:

$\ \mathbf{A} ( \mathbf{B C} ) = ( \mathbf{A B} ) \mathbf{C}.$

Matrix multiplication is distributive:

$\ \mathbf{A} ( \mathbf{B} + \mathbf{C} ) = \mathbf{A B} + \mathbf{AC}$

$\ ( \mathbf{A} + \mathbf{B} ) \mathbf{C} = \mathbf{A C} + \mathbf{B C}.$

Matrix multiplication is compatible with scalar multiplication:

$\ c ( \mathbf{A B} ) = ( c \mathbf{A} ) \mathbf{B}$

$\ ( \mathbf{A} c ) \mathbf{B} = \mathbf{A} ( c \mathbf{B} )$

$\ ( \mathbf{A B} ) c = \mathbf{A} ( \mathbf{B} c ).$

Note that matrix multiplication is not commutative:

$\ \mathbf{A B} \neq \mathbf{B A}.$

although, the order of multiplication can be reversed by transposing the matrices:

$\ \mathbf{A B} = \mathbf{(B^T A^T)^T}.$

[edit] Frobenius inner product

The Frobenius inner product, sometimes denoted A:B is the component-wise inner product of two matrices as though they are vectors. In other words, it is the sum of the entries of the Hadamard product, that is,

$\mathbf{A}:\mathbf{B}=\sum_i\sum_j A_{ij} B_{ij} = \operatorname{trace}(\mathbf{A}^T \mathbf{B}) = \operatorname{trace}(\mathbf{A} \mathbf{B}^T).$

This inner product induces the Frobenius norm.

[edit] Powers of matrices

Square matrices can be multiplied by themselves repeatedly in the same way that ordinary numbers can. This repeated multiplication can be described as a power of the matrix. Using the ordinary notion of matrix multiplication, the following identities hold for an n-by-n matrix A, a positive integer k, and a scalar c:

$\mathbf{A}^{0} = \mathbf{I}$

$\mathbf{A}^{k} = \prod_{i=1}^k \mathbf{A}$

$\ ( c\mathbf{A} )^k = c^k\mathbf{A}^k$

$\ \text{det} (A^k) = \text{det}(A)^k.$

The naive computation of matrix powers is to multiply k times the matrix A to the result, starting with the identity matrix just like the scalar case. This can be improved using the binary representation of k, a method commonly used to scalars. An even better method is to use the eigenvalue decomposition of A.

Calculating high powers of matrices can be very time-consuming, but the complexity of the calculation can be dramatically decreased by using the Cayley-Hamilton theorem, which takes advantage of an identity found using the matrices' characteristic polynomial and gives a much more effective equation for A^k, which instead raises a scalar to the required power, rather than a matrix.

[edit] See also

[edit] Notes

^ Matrix Multiplication
^ Press 2007, p. 108.
^ Knuth, 1998)
^ Robinson, 2005.
^ Eve, 2009.
^ (Horn & Johnson 1985, Ch. 5).

[edit] References

Henry Cohn, Robert Kleinberg, Balazs Szegedy, and Chris Umans. Group-theoretic Algorithms for Matrix Multiplication. arΧiv:math.GR/0511460. Proceedings of the 46th Annual Symposium on Foundations of Computer Science, 23-25 October 2005, Pittsburgh, PA, IEEE Computer Society, pp. 379–388.
Henry Cohn, Chris Umans. A Group-theoretic Approach to Fast Matrix Multiplication. arΧiv:math.GR/0307321. Proceedings of the 44th Annual IEEE Symposium on Foundations of Computer Science, 11-14 October 2003, Cambridge, MA, IEEE Computer Society, pp. 438–449.
Coppersmith, D., Winograd S., Matrix multiplication via arithmetic progressions, J. Symbolic Comput. 9, p. 251-280, 1990.
Eve, James. On O(n^2 log n) algorithms for n x n matrix operations. Technical Report No. 1169, School of Computing Science, Newcastle University, August 2009. PDF
Horn, Roger A.; Johnson, Charles R. (1985), Matrix Analysis, Cambridge University Press, ISBN 978-0-521-38632-6
Knuth, D.E., The Art of Computer Programming Volume 2: Seminumerical Algorithms. Addison-Wesley Professional; 3 edition (November 14, 1997). ISBN 978-0201896848. pp 501.
Press, William H.; Flannery, Brian P.; Teukolsky, Saul A.; Vetterling, William T. (2007), Numerical Recipes: The Art of Scientific Computing (3rd ed.), Cambridge University Press, ISBN 978-0-521-88068-8 .
Ran Raz. On the complexity of matrix product. In Proceedings of the thirty-fourth annual ACM symposium on Theory of computing. ACM Press, 2002. doi:10.1145/509907.509932.
Robinson, Sara, Toward an Optimal Algorithm for Matrix Multiplication, SIAM News 38(9), November 2005. PDF
Strassen, Volker, Gaussian Elimination is not Optimal, Numer. Math. 13, p. 354-356, 1969.

[edit] External links

The Wikibook Applicable Mathematics has a page on the topic of

Multiplying Matrices

The Simultaneous Triple Product Property and Group-theoretic Results for the Exponent of Matrix Multiplication
WIMS Online Matrix Multiplier
Matrix Multiplication Problems
Block Matrix Multiplication Problems
Matrix Multiplication in C
Linear algebra: matrix operations Multiply or add matrices of a type and with coefficients you choose and see how the result was computed.

[0] Matrix Multiplication

[1] Press 2007, p. 108.

[2] Knuth, 1998)

[3] Robinson, 2005.

[4] Eve, 2009.

[5] (Horn & Johnson 1985, Ch. 5).

[1]

[2]

[3]

[4]

[5]

[6]

Matrix multiplication

From Wikipedia, the free encyclopedia

Contents

[edit] Ordinary matrix product

[edit] Formal definition

[edit] Relationship with the inner product and the outer product

[edit] Properties

[edit] Algorithms for efficient matrix multiplication

[edit] Relationship to linear transformations

[edit] Scalar multiplication

[edit] Hadamard product

[edit] Kronecker product

[edit] Common properties

[edit] Frobenius inner product

[edit] Powers of matrices

[edit] See also

[edit] Notes

[edit] References

[edit] External links

Views

Personal tools

Navigation

Search

Interaction

Toolbox

Languages