IntroductionThe numerical methods of lines is a technique for solving partial differential equations discretizing in all but one dimension, and then integrating the semi-discrete problem as a system of ODEs or DAEs. A significant advantage of the method is that it allows the solution to take advantage of the sophisticated general purpose methods and software that have been developed for numerically integrating ODEs and DAEs. For the PDEs to which the method of lines is applicable, the method typically proves to be quite efficient. It is necessary that the PDE problem be well-posed as an initial value (Cauchy) problem in at least one dimension, since the ODE and DAE integrators used are initial value problem solvers. This rules out purely elliptic equations such as Laplace's equation, but leaves a large class of evolution equations that can be solved quite efficiently. A simple example illustrates better than mere words the fundamental idea of the method. Consider the following problem (a simple model for seasonal variation of heat in soil). This is a candidate for the method of lines since we have the initial value u(x,0)  0. 0. Problem (1) will be discretized with respect to the variable x using second order finite differences, in particular using the approximation Even though finite difference discretizations are the most common, there is certainly no requirement that discretizations for the method of lines be done with finite differences; finite volume or even finite element discretizations can also be used. To use the discretization above, choose a uniform grid  with spacing h with spacing h  1/n such that 1/n such that  . Let . Let 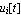 be the value of be the value of 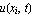 . For the purposes of illustrating the problem set-up, a particular value of n is chosen. . For the purposes of illustrating the problem set-up, a particular value of n is chosen. This defines a particular value of n and the corresponding value of h used in the subsequent commands. This can be changed to make a finer or coarser spatial approximation. In[3]:=  |
This defines the vector of  . . In[4]:=  |
Out[4]=

|
For 1 ≤ i ≤ 9, we can use the centered difference formula (2) to obtain a system of ODEs. However, before doing this, it is useful to incorporate the boundary conditions first. The Dirichlet boundary condition at x  0 can easily be handled by simply defining 0 can easily be handled by simply defining  as a function of t. An alternative option is to differentiate the boundary condition with respect to time and use the corresponding differential equation. In this example, the latter method will be used. as a function of t. An alternative option is to differentiate the boundary condition with respect to time and use the corresponding differential equation. In this example, the latter method will be used. The Neumann boundary condition at x  1 is a little more difficult. With second order differences, one way to handle it is with reflection: imagine we are solving the problem on the interval 0 ≤ x ≤ 2 with the same boundary conditions at x 1 is a little more difficult. With second order differences, one way to handle it is with reflection: imagine we are solving the problem on the interval 0 ≤ x ≤ 2 with the same boundary conditions at x  0 and x 0 and x  2. Since the initial condition and boundary conditions are symmetric with respect to x, the solution should be symmetric with respect to x for all time, and so symmetry is equivalent to the Neumann boundary condition at x 2. Since the initial condition and boundary conditions are symmetric with respect to x, the solution should be symmetric with respect to x for all time, and so symmetry is equivalent to the Neumann boundary condition at x  1. Thus, 1. Thus,  , so , so  This uses ListCorrelate to apply the difference formula. The padding  implements the Neumann boundary condition. implements the Neumann boundary condition. In[5]:=  |
Out[5]=

|
This sets up the zero initial condition. In[6]:= 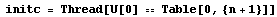 |
Out[6]=

|
Now the PDE has been partially discretized into an ODE initial value problem that can be solved by the ODE integrators in NDSolve. This solves the ODE initial value problem. In[7]:=  |
Out[7]=

|
This shows the solutions  plotted as a function of x and t. plotted as a function of x and t. In[8]:=  |
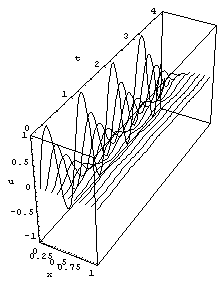
The plot above indicates why this technique is called the numerical "method of lines". The solution in between lines can be found by interpolation. When NDSolve computes the solution for the PDE, the result is a two-dimensional InterpolatingFunction. This uses NDSolve to compute the solution of the heat equation (1) directly. In[9]:=  |
Out[9]=
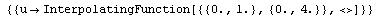
|
This creates a surface plot of the solution. In[10]:=  |

The setting n  10 used above did not give a very accurate solution. When NDSolve computes the solution, it uses spatial error estimates on the initial condition to determine what the grid spacing should be. The error in the temporal (or at least time-like) variable is handled by the adaptive ODE integrator. 10 used above did not give a very accurate solution. When NDSolve computes the solution, it uses spatial error estimates on the initial condition to determine what the grid spacing should be. The error in the temporal (or at least time-like) variable is handled by the adaptive ODE integrator. In the example (1), the distinction between time and space was quite clear from the problem context. Even when the distinction is not explicit, this document will refer to "spatial" and "temporal" variables. The "spatial" variables are those to which the discretization is done. The "temporal" variable is the one left in the ODE system to be integrated. Options for NDSolve`MethodOfLines. Use of some of these options requires further knowledge of how the method of lines works and will be explained in the sections that follow. Currently, the only method implemented for spatial discretization is the TensorProductGrid method, which uses discretization methods for one spatial dimension and uses an outer tensor product to derive methods for multiple spatial dimensions on rectangular regions. TensorProductGrid has its own set of options that you can use to control the grid selection process. The following sections give sufficient background information so that you will be able to use these options if necessary.
|